This calculator has not been completed as of March 2023. It also has a mathematical error in some routine that has yet to be found.
Taken from "Practical Astronomy With Your Calculator or Spreadsheet" 4th ed. by P. Duffett-Smith and J. Zwart.
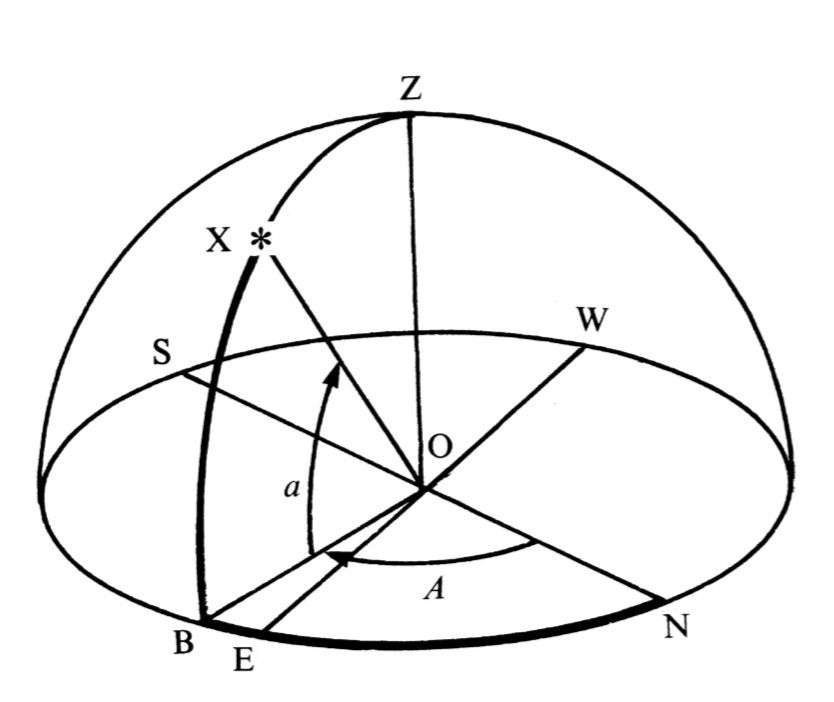
The horizon coordinates, azimuth and altitude, of an object in the sky are referred to the plane of the observer's horizon. Imagine an observer standing at point O; then his or her horizon is the circle NESW, where the letters refer to the north, east, south and west points of the horizon respectively. The direction north, by the way, relates to the direction of the north pole on the Earth's rotation axis and not to the magnetic north pole. You must imagine the stars as fixed on the surface of the hemisphere with the observer at the centre as shown below; the whole sphere of which this hemisphere is part is called the celestial sphere. The point Z directly over the observer's head is called the zenith; the direction OZ is the direction defined by a plumb line held by the observer. Now consider a star X and imagine a great circle (i.e. a circle drawn on the surface of the sphere whose centre is the same as that of the sphere) going through Z and X; it meets the horizon at point B. The altitude, a, of the star is then the angle subtended at O by the points X and B. The azimuth, A, is the angle subtended by the points N and B. Hence, the altitude is 'how far up' in degrees (negative if below the horizon) and the azimuth is 'how far round' from the north direction, also measured in degrees. A increases from 0° to 360° as you go around in the sense NESW, N being 0°, S being 180°, etc.
The altitudes and azimuths of all heavenly bodies except geostationary satellites are continually changing with time as the Earth rotates. This coordinate system then, marvelous for setting the direction of your telescope, is not much good for fixing the positions of the stars. Another frame of reference, independent of the Earth's motion, is needed to do that.
As their name suggests, these coordinates refer to the plane of the Earth's equator (see the Figure below). The observer (assumed to be in the northern hemisphere) is at O and the plane containing the circle NESW is again the horizon with Z the zenith point. You are to imagine now that the figure represents the view obtained at a vast distance from the Earth. The Earth, with the observer standing on it, has shrunk to a tiny dot at the centre of the diagram, but the plane of the equator has been extended to cut the celestial sphere along the circle EγRW. This is the equatorial plane and is inclined at the angle 90° - φ to the horizon, where φ is the observer's geographical latitude. For observations at latitude 52° N this angle is 38°. At right angles to the equatorial plane along the line OP lies the axis of rotation of the Earth; it intersects the celestial sphere at P, the north celestial pole, or north pole for short. Since this is the line about which the Earth spins, all the stars appear to describe circles in the sky about P.
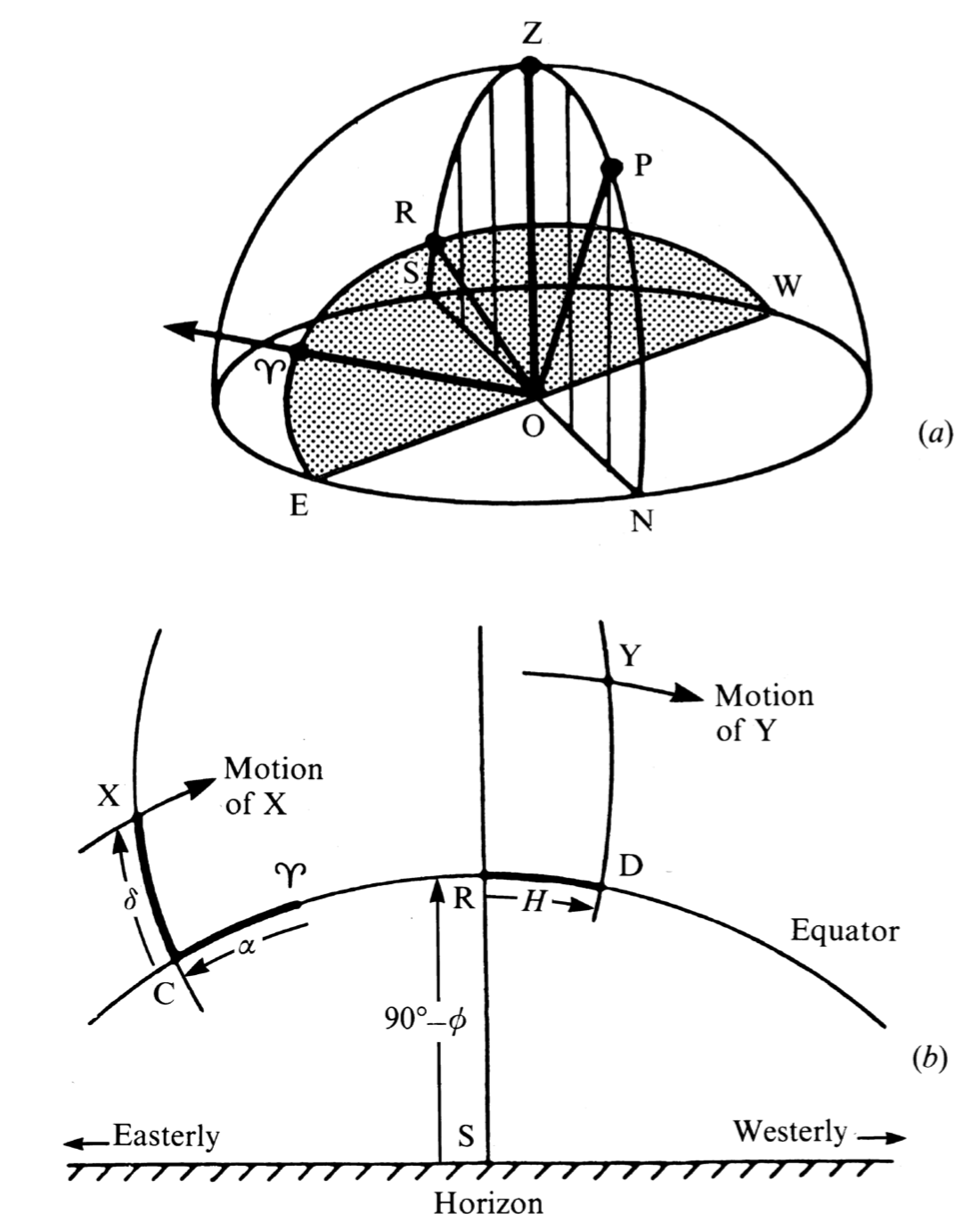
The figure shows two views: the celestial sphere and as seen from the ground. The lower picture shows the south point, S, of the horizon is marked and so is the imaginary trace of the equator, CγRD. The arc extending down through R and S is the great circle which goes through NPZRS in the top diagram. The arc extending down through XC is another great circle, not marked in the top, which goes through PXC. Consider the star at X. The arc CX, or the angle subtended at O by the points C and X, is called the declination, δ , of X, defining 'how far up' from, or north of, the equator. The other coordinate, 'how far round', is defined with respect to a fixed direction in the sky, marked by the symbol γ. This direction, called the vernal equinox or the first point of Aries, lies along the line of the intersection of the plane of the Earth's equator with that of the Earth's orbit around the Sun. But we needn't worry about such definitions at the moment. All we need to know is that the direction γ remains fixed with respect to the stars except for the effects of precession and nutation (discussed later), and that we measure the other coordinate with respect to it. This coordinate is called the right ascension, α, and is the angle subtended at O by the points γ and C.
Throughout the course of the day the star X moves steadily westwards along a circle centered on P, completing one revolution in 24 hours of sidereal time . Since this circle is a circle parallel to that of the equator the declination does not change. Furthermore, since the direction γ is fixed in the heavens, it appears to move along the equator at exactly the same rate as X moves along the circle. Hence the right ascension does not change either. Thus α and δ are ideal coordinates for describing the positions of the stars and other 'fixed' heavenly bodies.
Related to the right ascension is another 'how far round' coordinate called the hour angle, H. For the star Y it is defined as the angle subtended at O by the points R and D and is a measure of how far the star has travelled along the equator from the southern point R, that is a measure of the time since it crossed the meridian. H increases uniformly as the day proceeds; when H is zero, the star crosses the great circle NPZRS (upper figure). This circle is called the meridian and the star is said to transit or culminate. Its altitude is then maximum and its azimuth is 180° (provided that its declination is less than the geographical latitude).
The declination is measured in degrees, positive north of the equator and negative south of it. The hour angle and the right ascension may also be measured in degrees, 0° to 360°. α is measured in the sense that it increases as you move east from γ; the point γ itself is at 0°. (Note that this is in the opposite sense to that in which H is measured.) More commonly, however, these two coordinates H and α are measured in hours, minutes and seconds of time from 0 to 24 hours. One complete revolution, 360°, corresponds to 24 hours of sidereal time; thus 1 hour is equivalent to 15°. The two statements 'the right ascension of X is 90°' and 'the right ascension of X is 6 h' are entirely equivalent. To convert from one to the other simply multiply or divide by 15.
A useful result of measuring the right ascension in time is that the star transits when the local sidereal time is equal to the right ascension.
The plane containing the Earth's orbit around the Sun is called the ecliptic and the other planets in our Solar System also move in orbits close to this plane. When making calculations on objects in the Solar System it is therefore often convenient to define positions with respect to the ecliptic, that is, to use the ecliptic coordinate system. This system, like the equatorial system described above, also uses the vernal equinox, γ, as its reference direction. The figure below, which is similar to the Equatorial diagram above, shows how it goes.
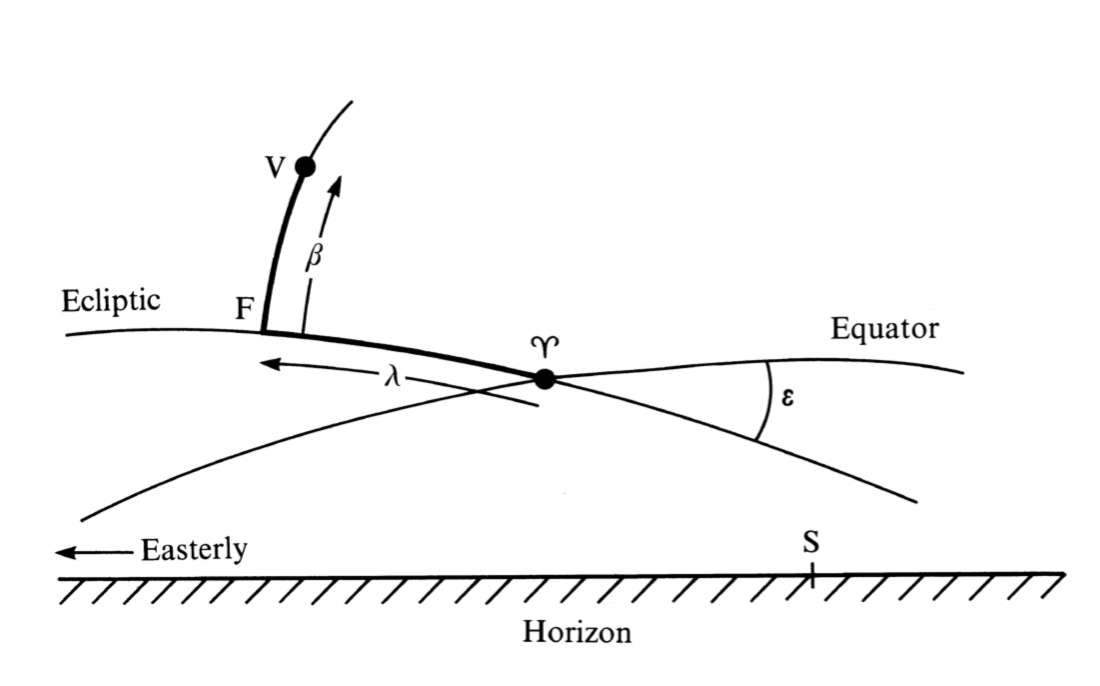
The imaginary traces of the planes of the equator and the ecliptic are drawn on the sky, and their point of intersection is the vernal equinox, γ. The two planes are inclined to each other at an angle of about 23.5 degrees, called the obliquity of the ecliptic and given the symbol ε. (See Section 27 for a formula for calculating ε.) This angle is the tilt of the Earth's NS axis from the perpendicular to the plane of the ecliptic. Also marked in the diagram is a planet, V. Part of the trace of the imaginary great circle from the pole of the ecliptic (i.e. the point where the line drawn through the Sun perpendicular to the ecliptic meets the celestial sphere) down through V is marked and this cuts the ecliptic at F. Then the ecliptic longitude, λ, of V is defined to be the angle subtended by the points γ and F, and the ecliptic latitude, β , the angle subtended by the points F and V.
As with equatorial coordinates, β is positive if the planet is above (i.e. north of) the ecliptic and negative if it is below it. The sense of λ is such that λ increases as you move eastwards along the ecliptic. Both λ and β are usually measured in degrees.
During the course of the year the Sun moves eastwards along the trace of the ecliptic. By definition, its ecliptic latitude is always zero. On about 21 March, it is at the position γ and its right ascension and declination are both zero. Its ecliptic longitude is also zero. Thereafter, its ecliptic longitude steadily increases until three months later it is 90°, midsummer in the northern hemisphere. After the course of 1 year, the Sun has returned to its starting position having traversed 360° of ecliptic longitude.
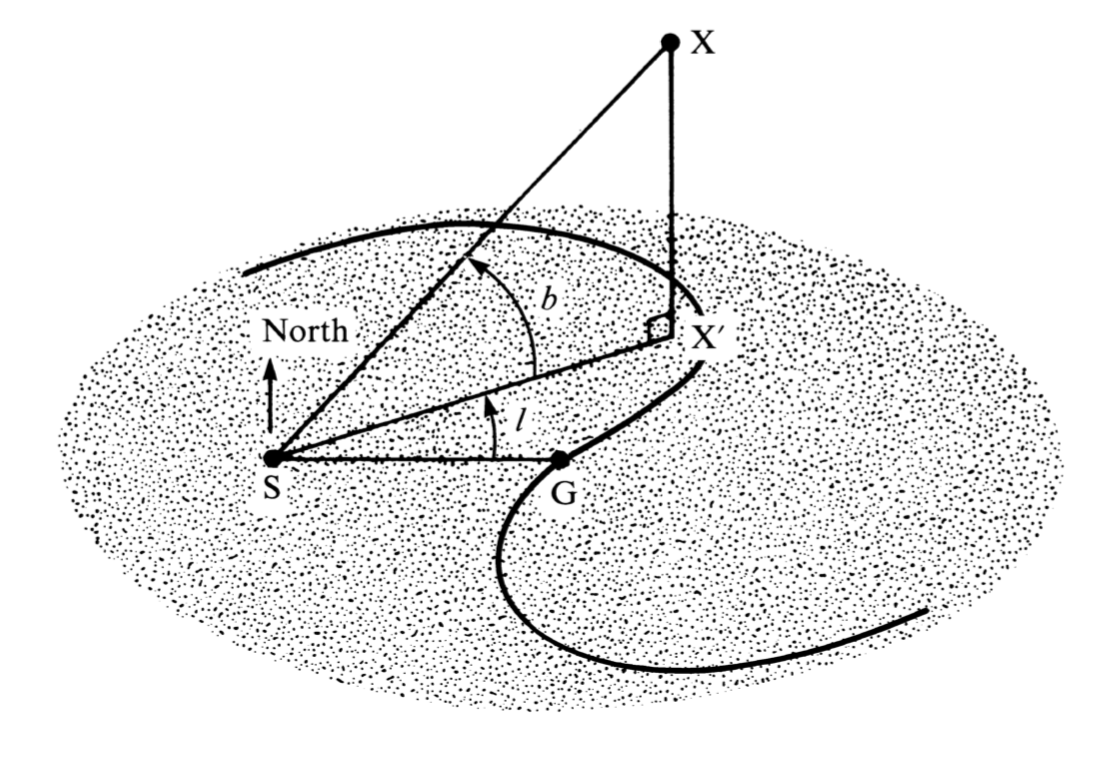
Astronomers occasionally need to describe the relationships between stars or other celestial objects within our own Galaxy and to do so it is convenient to use the galactic coordinate system. This time, the fundamental plane is the plane of the Galaxy and the fundamental direction is the line joining our Sun to the centre of the Galaxy. The diagram below describes the situation. The point marked S represents the Sun, G is the centre of the Galaxy, and X a star which does not lie in the galactic plane. In equatorial coordinates, the position of G is α = 17h 42.4m and δ = -28° 55'. The lines SG and SX' both lie in the plane of the Galaxy; the point X' is the projection of the star's position onto the plane. The galactic longitude is defined to be the angle l measured in the plane, and the galactic latitude is defined to be the angle b measured perpendicular to it. The longitude increases from 0° to 360° in the same direction as increasing right ascension, and the latitude ranges from 0° to 90° north of the plane and from 0° to -90° south of it. These coordinates may be used, for example, to express the position of a star in the Milky Way.
It is common astronomical practice to express the hour angle or right ascension of a star in hours, minutes and seconds of time rather than in degrees. We can transform one to the other by noting that 360° of Earth's rotation takes place in 1 day, or 24 hours. Thus 360° is equivalent to 24 hours or 15° to 1 hour. To convert between angles expressed in decimal hours and angles expressed in decimal degrees, simply multiply or divide by 15. For example, the right ascension 9h 36m 10.2s is equivalent to 144° 02' 33''.
The hour angle, H, and the right ascension, α, are related by the simple formula:
where LST is the local sidereal time. All quantities must be expressed in the same units, i.e. as degrees or as hours. (Longitudes West are entered as negative numbers.)